Vision Transformers in Words and Code :: Draft

Introduction #

The Vision Transformer is a remarkably simple but powerful vision model. It was introduced in “An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale” by Google Brain in 2020 (Dosovitskiy et al.) At the time it was published, this paper obtained SOTA on ImageNet classificiation, while using less compute than the prior state of the art.

Image classification performance

The main idea is to view an image as a sequence of “patches,” smaller subregions that make up the image. Once we have a sequence of patch-level embeddings, we can leverage ideas from sequence modeling in NLP to encode it with a transformer. For image classification, we can add an MLP head to map the transformer embedding to $N$ classes. Vision Transformers have also been applied to a wide range of tasks, including detection, segmentation and monocular depth estimation.

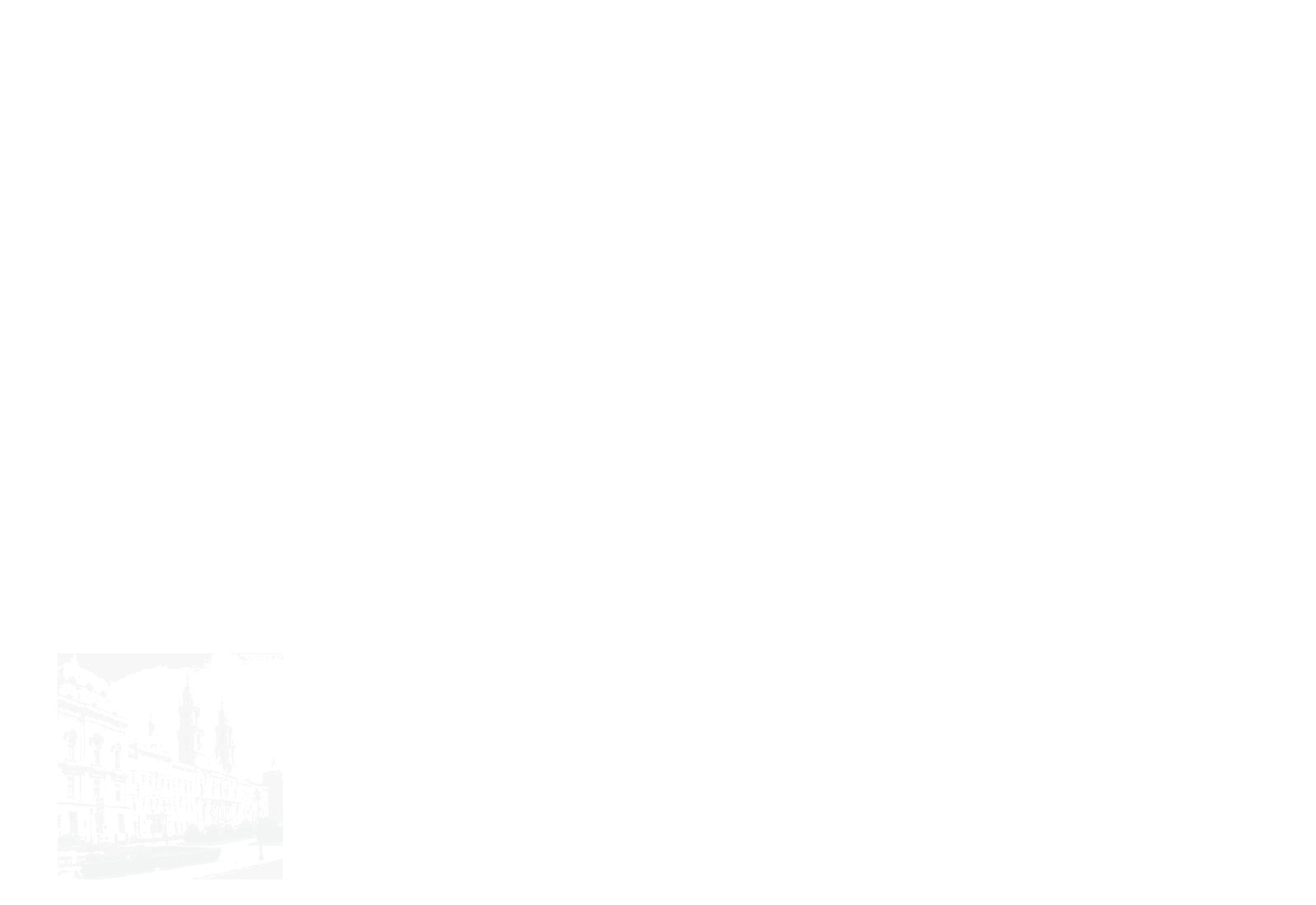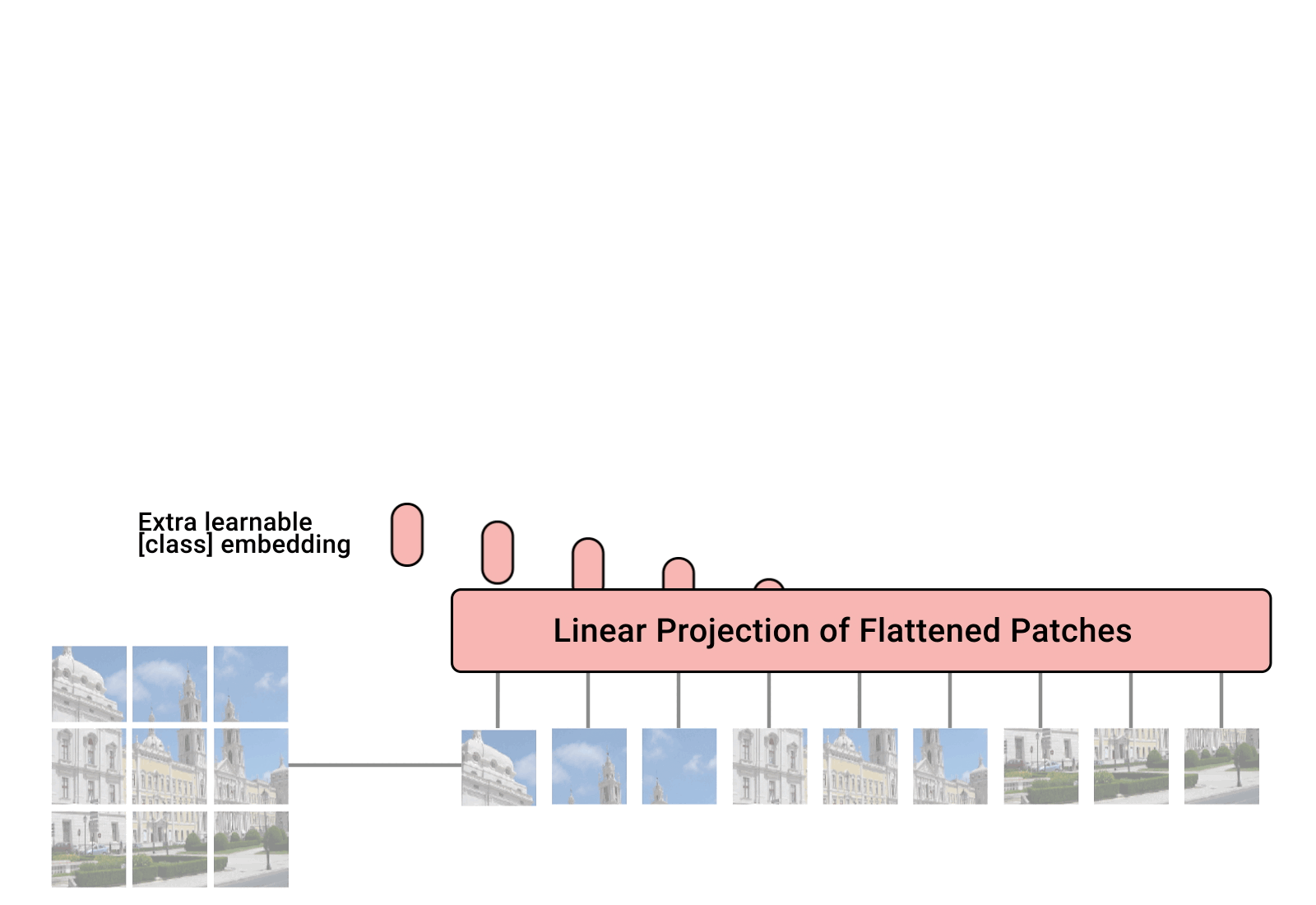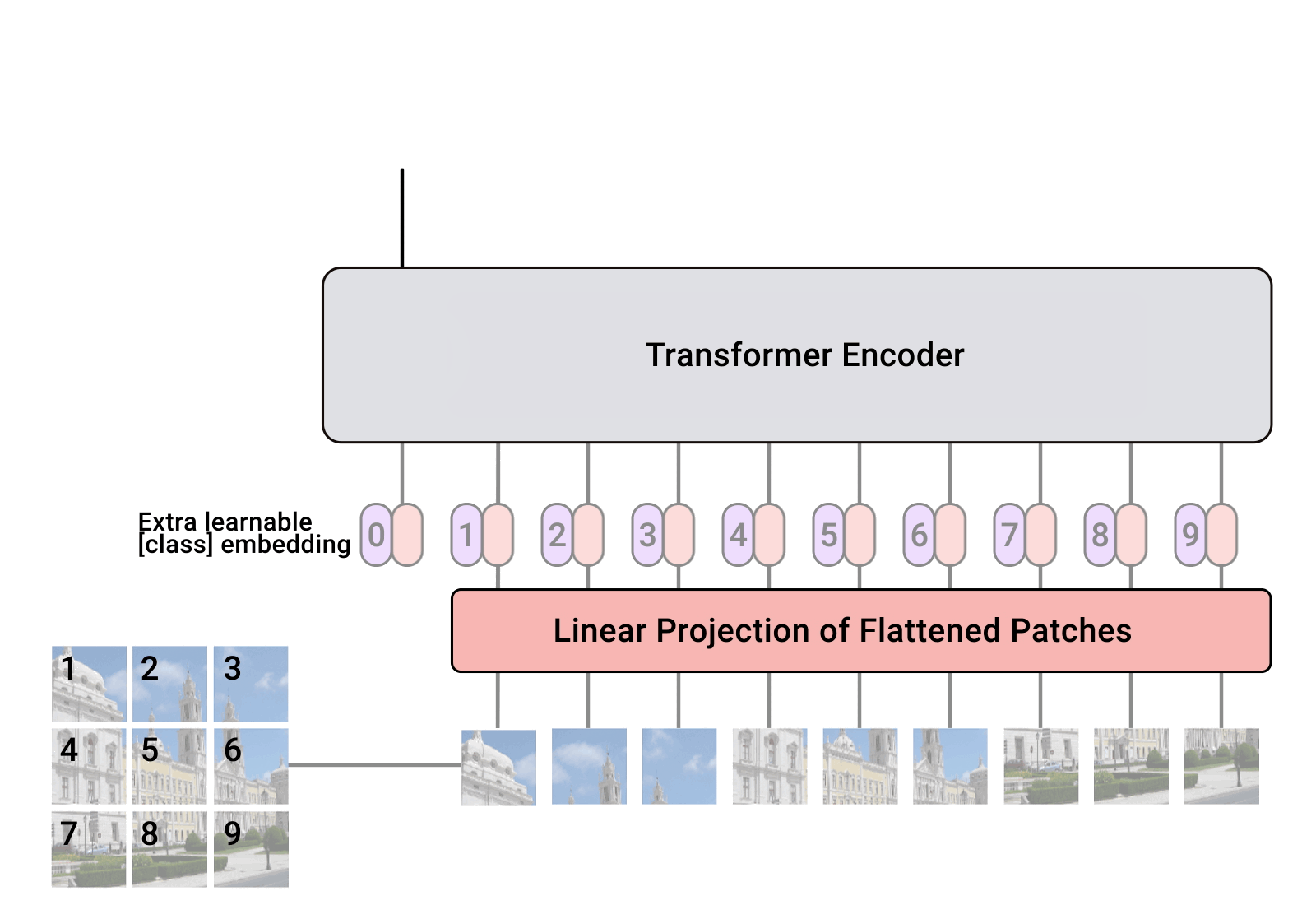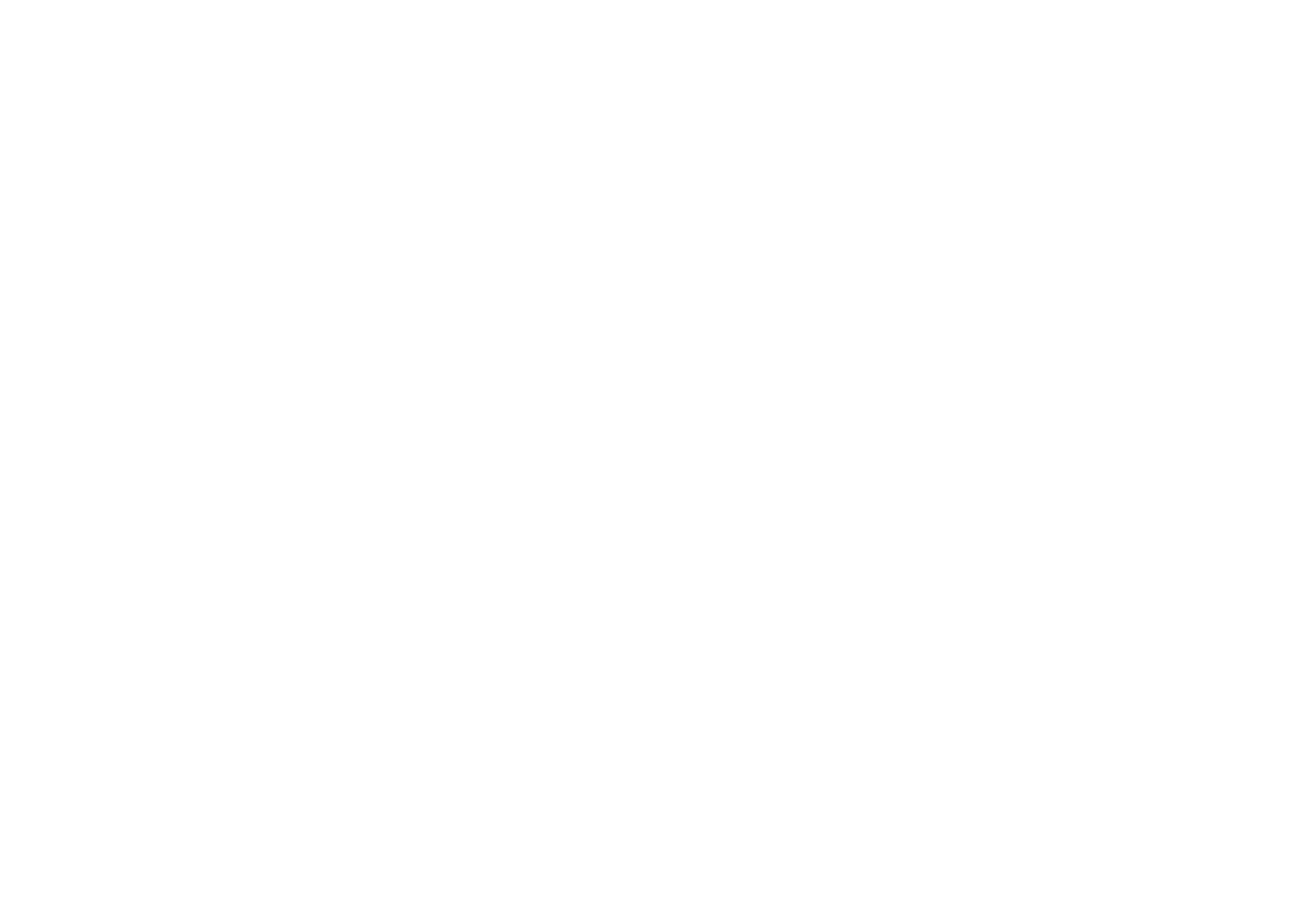
Vision transformer animation

Model Architecture #

We will focus on the architecture of google/vit-base-patch16-224, the original model released by Google in this repository. It was pre-trained on ImageNet-21k (14 million images, 21,843 classes) at resolution 224 x 224, and fine-tuned on ImageNet 2012 (1 million images, 1000 classes) at resolution 224 x 224.

The model architecture can be broken down into 5 components:

Patchify and embed the image
Add positional encodings
Transformer Encoder
Pooling
MLP head

Patchify the image #

We will start by patchifying the image. This means dividing an $n \times n$ image into chunks of size $k \times k$ , and embedding each chunk with a linear layer. This lets us model the image as a “sequence of patches” and apply the usual toolbox of transformers to them.

To indicate the beginning of an image, we will prepend a learnable “cls” token to the input, following the technique applied in BERT.


self.to_patch_embedding = nn.Sequential(
    Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1 = patch_height, p2 = patch_width),
    nn.LayerNorm(patch_dim),
    nn.Linear(patch_dim, dim),
    nn.LayerNorm(dim),
)

Add positional encodings #

Since transformers are invariant to the order in which the input is presented to them, we need to add positional encodings to the patch embeddings. Before doing this, we will also prepend the cls token to the input as discussed above.


cls_tokens = repeat(self.cls_token, '1 1 d -> b 1 d', b = b)
x = torch.cat((cls_tokens, x), dim=1)
x += self.pos_embedding[:, :(n + 1)]

Transformer encoder #


x = self.transformer(x)

The self.transformer object is a vanilla transformer encoder that looks like this:


class FeedForward(nn.Module):
    def __init__(self, dim, hidden_dim, dropout = 0.):
        super().__init__()
        self.net = nn.Sequential(
            nn.LayerNorm(dim),
            nn.Linear(dim, hidden_dim),
            nn.GELU(),
            nn.Dropout(dropout),
            nn.Linear(hidden_dim, dim),
            nn.Dropout(dropout)
        )

    def forward(self, x):
        return self.net(x)

class Attention(nn.Module):
    def __init__(self, dim, heads = 8, dim_head = 64, dropout = 0.):
        super().__init__()
        inner_dim = dim_head *  heads
        project_out = not (heads == 1 and dim_head == dim)

        self.heads = heads
        self.scale = dim_head ** -0.5

        self.norm = nn.LayerNorm(dim)

        self.attend = nn.Softmax(dim = -1)
        self.dropout = nn.Dropout(dropout)

        self.to_qkv = nn.Linear(dim, inner_dim * 3, bias = False)

        self.to_out = nn.Sequential(
            nn.Linear(inner_dim, dim),
            nn.Dropout(dropout)
        ) if project_out else nn.Identity()

    def forward(self, x):
        x = self.norm(x)

        qkv = self.to_qkv(x).chunk(3, dim = -1)
        q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h = self.heads), qkv)

        dots = torch.matmul(q, k.transpose(-1, -2)) * self.scale

        attn = self.attend(dots)
        attn = self.dropout(attn)

        out = torch.matmul(attn, v)
        out = rearrange(out, 'b h n d -> b n (h d)')
        return self.to_out(out)

class Transformer(nn.Module):
    def __init__(self, dim, depth, heads, dim_head, mlp_dim, dropout = 0.):
        super().__init__()
        self.norm = nn.LayerNorm(dim)
        self.layers = nn.ModuleList([])
        for _ in range(depth):
            self.layers.append(nn.ModuleList([
                Attention(dim, heads = heads, dim_head = dim_head, dropout = dropout),
                FeedForward(dim, mlp_dim, dropout = dropout)
            ]))

    def forward(self, x):
        for attn, ff in self.layers:
            x = attn(x) + x
            x = ff(x) + x

        return self.norm(x)

Pooling and MLP #

Finally, we will apply optional pooling followed by an MLP.


x = x.mean(dim = 1) if self.pool == 'mean' else x[:, 0]
x = self.to_latent(x)
return self.mlp_head(x)

Comparison to ConvNets #

An interesting point the paper makes is that vision transformers perform worse than ConvNets when trained on small datasets, but they outperform ConvNets when very large datasets are used.

Inference Code #

The full inference code for the vision transformer can be found here. This implementation is adapted from Phil Wang’s excellent repo, with some modifications to let us load a pretrained model and show that the outputs are equivalent.