Decision making reduces to prediction :: Draft

One idea that is well known in reinforcement learning is that good decision making reduces to good prediction. Lately I’ve been working on RL at work, which made me reflect on this concept and its connections to everyday life. Whether you’re a recent graduate trying to figure out what job to take, or a CEO trying to pick a direction for a company, the quality of our decisions shapes the trajectory of our lives. So it’s important to figure out how to get better at making decisions under uncertainty.

There are many deep RL algorithms, but here we’ll think about $Q$ learning because it’s simple and general. In Q-learning, the function $Q^{\pi}(s, a)$ represents the expected discounted cumulative reward when starting in state $s$, taking action $a$, and thereafter following policy $\pi$: $$ Q^\pi(s, a)=\mathbb{E}_\pi\left[\sum_{t=0}^{\infty} \gamma^t r\left(s_t, a_t, s_{t+1}\right) \mid s_0=s, a_0=a\right] $$

Suppose we have a policy $Q_{\theta}(s, a)$ parametrized by a neural network. A natural decision making policy is to take the action that maximizes $Q$: $$ a_t = \text{argmax}_{a} Q_{\theta}(s, a) $$

This means that most of the heavy lifting in decision-making is in prediction, in the $Q$ function. That is, the quality of an agent’s decisions in the RL framework is equivalent to the quality of its ability to make predictions about the environment. When making decisions, it follows that the way to make better decisions is to make better predictions about the world.

How does one get better at this? I think it follows from experience and reflection. When you take actions in the world and observe the results, you can fit a world model. Experience is necessary to collect “training examples,” while reflection is needed to interpret experience and bake it into a better world model. The mind does this subconsciously for certain decisions – we’re more likely to visit a restaurant where we previously had a good experience. But for other decisions like deciding the strategy of a company, a more deliberate process of reasoning and reflection from past experience may be necessary.

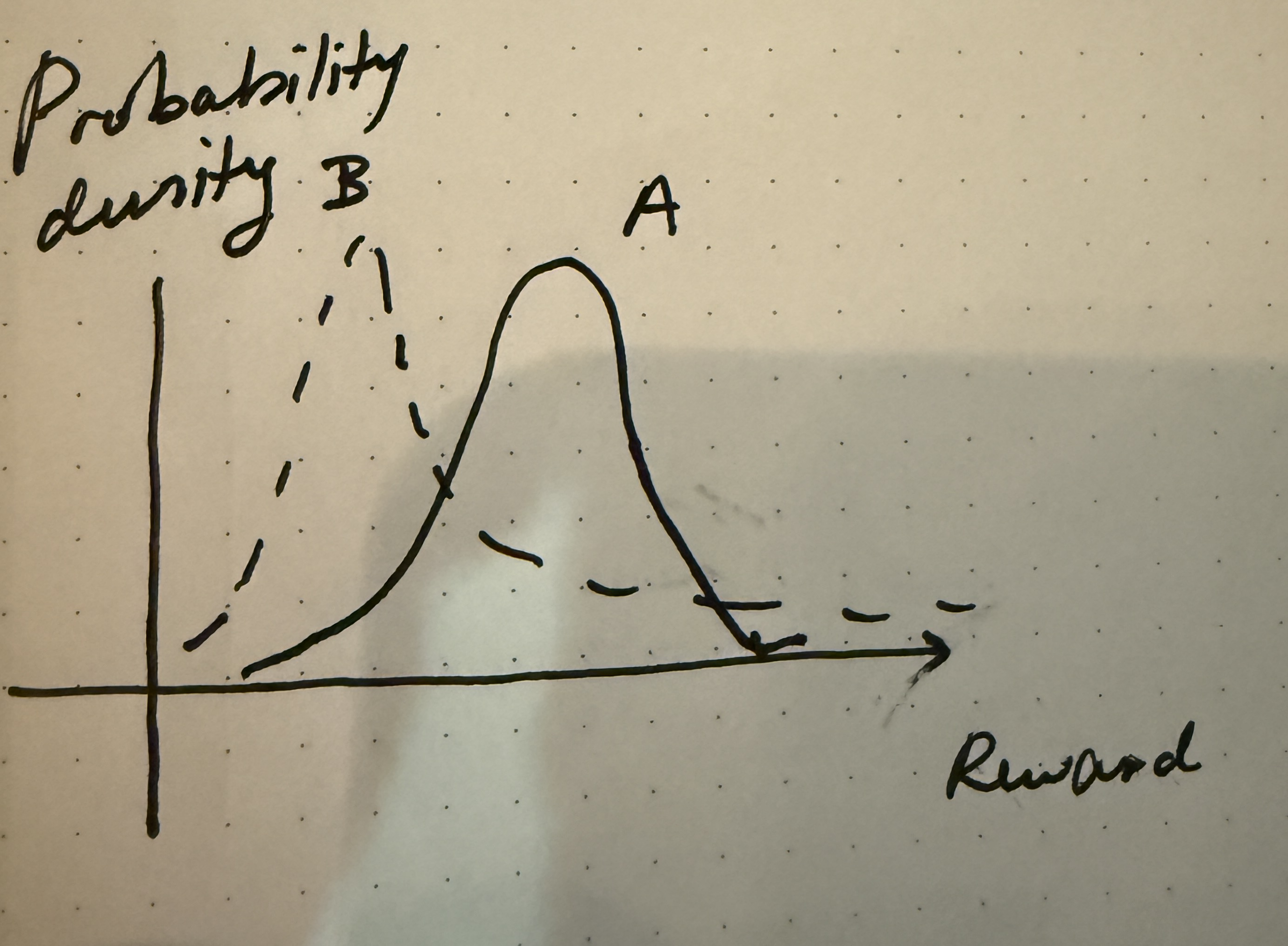
Much of the time, decisions need to be made under uncertainty. Suppose we have two possible choices, $A$ and $B$, drawn below. Each curve represents a probability distribution over outcomes, with the $x$-axis denoting some notion of reward or goodness, and the $y$-axis denoting probability density. Assuming that $A$ and $B$ are normal distributions with the same variance, it’s obvious that it makes sense to pick $B$. It’s not always the case that picking $B$ will have a better outcome than $A$, but on average you’ll be better off picking $B$.

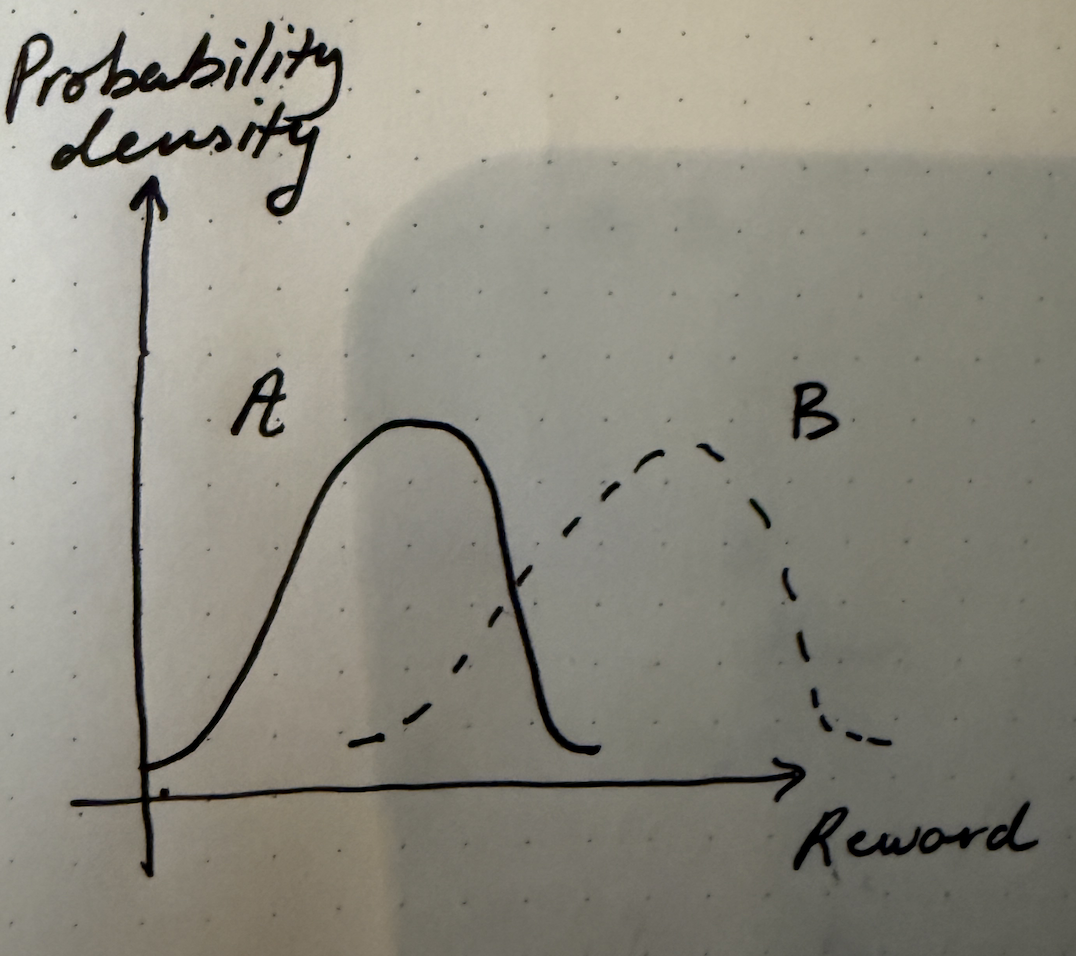
A more interesting case is when you have two choices like the following. Here, the expected reward from picking $A$ is higher than picking $B$, but the variance of $B$ is higher. A real-life example that parallels this is joining a startup vs. joining a big company. Reward here can either represent compensation or some more abstract notion that combines compensation, life satisfiction, learning, among other factors. On average, in this diagram, joining a bigger company has higher reward, but it can still make sense to join a startup because of the possibility of tail outcomes.

Another tricky question is how to pick a reward function. In most decisions, it’s hard to write down an explicit formula that maps a choice to a numerical value. But we still have a latent preference function that can often tell us whether one scenario is preferable to another. Figuring out the right reward function is as important as making predictions about it.

What makes decisions hard? It mostly comes down to uncertainty. A distinction I find useful here is the difference between epistemic uncertainty and aleatoric uncertainty. Epistemic uncertainty refers to uncertainty due to lack of knowledge. This is something that can be improved through more experience or learning. Aleatoric uncertainty refers to uncertainty that arises due to the inherent randomness of the environment. This is generally not reducible.

Knowing which kind of uncertainty you are dealing with is very helpful, because it can help inform how to respond to it. For epistemic uncertainty, the appropriate response is probably collecting more information. For aleatoric uncertainty, one probably needs to accept a certain amount of randomness in the environment, and hedge or make preparations for the worst case. I first learned about these forms of uncertainty from “What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision?”, a great paper by Alex Kendall and Yarin Gal. Here’s a nice image that illustrates this point:

Great decision makers, individuals who can make difficult choices with limited information in high-stakes situations, are hard to replicate. And the way to make better decisions is to pick a reward function, and learn to make really good predictions. If you can do that, then decision-making becomes an easy as taking the argmax.